Link to MathSciNet Review MR2841564 . " This presentation of what can be thought of as the semi-abelian model is a valuable contribution to the literature; as indicated in the final chapter, there are abundant areas for future study."

Link to Review in Jahresber. Deutsch. Math.-Verein. 114 (2012), 177 - 182 . "Nonabelian phenomena play as well a major role in algebraic geometry (Brauer-Severi varieties, Teichmüller groupoid, etc., to list a few instances). It may well be that, in the future, the ideas presented in the book contribute to some of the many open questions in these areas."

Link to Review in Zentrallblatt Zbl 1237.55001 .

Table of Contents

• Preface
• Prerequisites and reading plan
• Historical Context Diagram
• Introduction
• Part I. 1- and 2-dimensional results
1. Introduction to Part I
2. History
3. Homotopy theory and crossed modules
4. Basic algebra of crossed modules
5. Coproducts of crossed P-modules
6. Induced crossed modules
7. Double groupoids and the 2-dimensional Seifert-van Kampen Theorem
• Part II. Crossed complexes
8. Introduction to Part II
9. The basics of crossed complexes
10. The higher homotopy Seifert-van Kampen Theorem (HHSvKT) and its applications
11. Tensor products and homotopies of crossed complexes
12. Resolutions
13. The cubical classifying space of a crossed complex
14. Nonabelian cohomology: spaces, groupoids
• Part III. Cubical ω-groupoids
15. Introduction to Part III
16. The algebra of crossed complexes and cubical ω-groupoids
17. The cubical homotopy ω-groupoid of a filtered space
18. Tensor products and homotopies
19. Future directions?
• Appendices
• Bibliography
• Glossary of symbols
• Index

Download of Introduction 0.15MB

Link to `Higher dimensional group theory'.

Further details

This book gives in one place a full account of a theory which, without using singular homology theory or simplicial approximation, but employing filtered spaces and methods analogous to those used originally for the fundamental group or groupoid, obtains for example:

1. the Brouwer degree theorem;
2. the Relative Hurewicz theorem, seen as a special case of a homotopical excision theorem giving information on relative homotopy groups as a module over the fundamental group;
3. nonabelian information on second relative homotopy groups of mapping cones, and of unions: these results are not available through traditional methods;
4. homotopy information on the space of pointed maps X → Y when X is a CW-complex of dimension n and Y is connected and has no homotopy between 1 and n; this result again involves the fundamental groups and their actions.

To compare the work needed for this with that for traditional approaches, the two papers published in Journal of Pure and Applied Algebra, 1981, ([31,32] of my publication list) which obtained the first three of the above results amounted to 59 pages, and used only basic facts on CW-complexes, and cubical sets; the nonabelian results of 3. are not available by traditional methods.

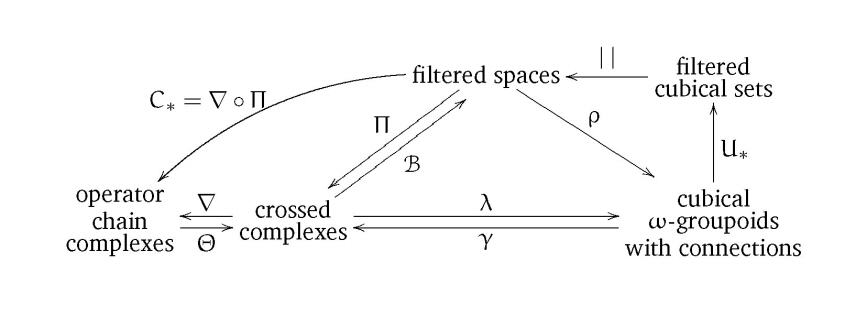
These results are possible by working directly with two functors defined homotopically on filtered spaces, the fundamental crossed complex, Π, which goes back to Blakers and Whitehead (1949), and the fundamental cubical homotopy ω-groupoid, ρ. A central aspect is a Higher Homotopy van Kampen Theorem, which is:

• proved using ρ ;
• is applied through Π ;
• and allows some direct colimit calculations of relative homotopy groups.

The contrast between Π and ρ is seen clearly in dimension 2. Both are defined for a triple (X,A,C) of spaces in which C is a set of base points in A which is itself a subspace of X. The seond relative homotopy group of this triple is the bundle of groups over C each group consisting of homotopy classes of maps of a square into X which take one chosen edge to A and the other three edges to c in C. Composition is in one direction only. Thus the definition involves a choice, and is unsymmetric. It is easy to prove that the composition structure is well defined and gives a bundle of groups. The proof that one obtains a crossed module over the fundamental groupoid of (A,C) is less straightforward.

By contrast, the homotopy double groupoid ρ of the triple is given by the natural and aesthetic definition that it consists of homotopy classes rel vertices of maps of a square into X which take the edges into A and the vertices into C. Compositions are in both directions, but the proof that these are well defined is non trivial, as is the proof of the relation with the second relative homotopy group.

The great advantage is that this construction allows algebraic inverses to subdivision, and the notion of commutative cube, both necessary for the proof of the 2-dimensional van Kampen theorem. Aesthetic implies power!

This theory does not replace homology theory, but it does reach aspects of the subject not obtainable by that theory, particularly areas involving the operations of the fundamental group or groupoid, and nonabelian results on second relative homotopy groups, even on homotopy 2-types. Thus there is much work to be done to develop the interrelations.

The papers which give this theory were developed over the period 1971-2001. For a survey of the material to be contained in the book, see the article
 `Crossed complexes and homotopy groupoids as non commutative tools for higher dimensional local-to-global problems', Proceedings of the Fields Institute Workshop on Categorical Structures for Descent and Galois Theory, Hopf Algebras and Semiabelian Categories, September 23-28, Fields Institute Communications 43 (2004) 101-130 (see updated version  to appear in Michiel Hazewinkel (ed), Handbook of Algebra vol 6, Elsevier (2009)). It will be seen from this article, that the structures which enable the full use of crossed complexes as a tool in algebraic topology are substantial, intricate and interrrelated.

A major result, generalising classical results of Eilenberg-Mac Lane, and using all the tools developed, is the homotopy classification of maps from a CW-complex to the classifying space BC of a crossed complex C.  Recent work has further shown the utility of the classifying space for the homotopy classification of maps, relating the classical group theory of abstract kernels, and their obstructions to extensions,  with mappings of an n-dimensional space into a space whose homotopy vanishes between 1 and n. Here the notion of fibration of crossed complexes and related exact sequences gives a view of basic obstruction theory.

The power behind these methods comes from the cubical ω-groupoids, which form a convenient category to obtain a monoidal closed structure, and to express both `algebraic inverses to subdivision, and the definition of, and compositions of, commutative cubes', both essential for the local-to-global colimit results (Higher Homotopy van Kampen Theorem).

It is hoped that this exposition will help progress towards Grothendieck's vision of nonabelian cohomology.

Since the globular case is currently favoured for higher category theory, it might be asked:
                      `Why are there not globular ω-groupoids in the above diagram?'
The answer is that it was early proved with Higgins that they are equivalent to crossed complexes, but we were unable to do anything with them, either calculate, as we can with crossed complexes, or conjecture and prove theorems, as we can with the cubical case.  Functors from simplicial sets or cubical sets to crossed complexes are well studied and applied.  In these cases, the notion of free crossed complex is central to the applications, but hardly appears in the globular case. The globular ω-groupoid on one free generator of dimension n is analysed (probably for the first time!) in a recent paper to appear in HHA  on a higher homotopy globular ω-groupoid of a filtered space (pdf).

To present an integrated view of the structures hinted at in the Main Diagram has required no essential change in the detailed proofs, but has needed reordering of the material, some extra clarification, and redrafting for consistency. Also there were some research problems to extend the theory. For example the theory of acyclic models presented problems with normalisation for the fundamental crossed complex of a simplicial set. This has now been resolved in a paper in JHRS.

Recently, it has been decided that the simplicial classifying space theory is a bit of a diversion from the main cubical thrust, and so we are returning to the spirit of a previous cubical version of the classifying space, which dates back to 1982. An advantage of the cubical theory is that proofs are simpler, because the cubical Eilenberg-Zilber map is an isomorphism. Recent accounts of the homotopy theory of cubical sets are also helpful in this respect.

There are new expositions of calculating colimits in modules and crossed modules over groupoids, and calculating the tensor product of crossed complexes. So the order of material has changed from previous versions.

It is interesting that there is still scepticism that a reworking of basic algebraic topology, returning to some intuitive roots in this way, is possible. Indeed the applications of groupoids in algebraic topology and combinatorial group theory are not widely accepted. The 2-dimensional van Kampen theorem is not referred to even in some books or papers using or proving some of its easy consequences, such as Whitehead's theorem on free crossed modules, for which methods not directly involved with the universal property of a free object seem preferred.

It is helpful that the preparatory book `Topology and Groupoids' is now available, for which here is a link to a review. The work on the 1968 version of this book convinced the author that all of 1-dimensional homotopy theory is better expresed by consistently using groupoids, as this led to more powerful theorems with simpler proofs (which seems OK to some of us; perhaps perceptively, a reviewer of that edition for the MAA wrote that `it reads like a book on topology written by a category theorist', and in any case these uses of groupoids were largely ignored by algebraic topologists for 3 decades). The natural question arose:

                         Can the success of groupoids in 1-dimensional homotopy theory be extended to higher homotopy theory?

This required development of the algebra of double groupoids and 11 years work to develop the notion of higher homotopy groupoid. As P.A. Dirac said in one of his last addresses, but thinking primarily about physics: `.....one must follow up a mathematical idea and see what its consequences are, even though one gets led to a domain which is completely foreign to what one started with.... ' . This contrasts with the often current emphasis on the conformist notion of `the mainstream'. A natural reply to those who taunt `Not mainstream!' is: `Not yet!' Indeed, the head of the BBSRC, commented (THES, Oct 2008) that there is a difference between `mainstream' and `cutting edge'.

Philip Higgins' name is on the book in view of his large and inseparable input to the research, with his intuition, algebraic expertise and expository skills, though the responsibility for the correctness of the final version will still reside with the other two!  

One overall theme of this book is the use for the foundations of algebraic topology of some higher categorical structures, which allow for the application of
                                        higher dimensional nonabelian methods to certain local-to-global problems.
 Here is a link to an update of the proposal   (pdf)     (or html) for a Leverhulme Emeritus Fellowship which supported this project.

From the Preface:

`Our aim for this book is to give a connected and we hope readable account of the main features of work on extending to higher dimensions the theory and applications of the fundamental group.'

`We describe algebraic structures in dimensions greater than 1 which develop the nonabelian character of the fundamental group: they are in some sense `more nonabelian than groups', and they reflect better the geometrical complications of higher dimensions than the known homology and homotopy groups. We show how these methods can be applied to determine homotopy invariants of spaces, and homotopy classification of maps, in cases which include some classical results, and allow results not available by classical methods.'

`In Part I we give some history of work on the fundamental group and groupoid, in particular explaining how the Seifert-van Kampen theorem gives a method of computation of the fundamental group. We are then mainly concerned with the extension of this nonabelian work to dimension 2, using the key concept, due to J.H.C. Whitehead in 1946, of crossed module.'

`In Part II we extend the theory of crossed modules to crossed complexes, giving applications which include many basic results in homotopy theory, such as the relative Hurewicz theorem. This Part is intended as a kind of handbook of basic techniques in this border area between homology and homotopy theory.'

`However for the proofs of these results, particularly of the Higher Homotopy Seifert-van Kampen theorem, and of the use of the tensor product and homotopy theory of crossed complexes, i.e. monoidal closed structures, we have to introduce in Part III another algebraic structure, that of cubical ω-groupoids with connections,' and to prove its equivalence with crossed complexes. This equivalence algebraicises some long standing geometric methods or intuitions in relative homotopy theory.

For some recent papers relating to this work see [152,162,166,168] of my publication list. For seminars and conference presentationson in this area see my preprint page.

It is a pleasure to acknowledge that the writing of this book was supported by a Leverhulme Emeritus Fellowship, 2002-2004. This link gives details of the proposal for support>.

Errata

Revised: December 1, 2016